次の手順は、数値 6 の因数ペアを見つける方法を示しています。 1×6＝6 2×3＝6 3×2＝6 6×1＝6 ペアをリストするとき、同じ要因を繰り返さないため、要因ペアは次のように与えられます。 (1,6) (2,3) すべての数には同様に正と負の要因があり、負のペア
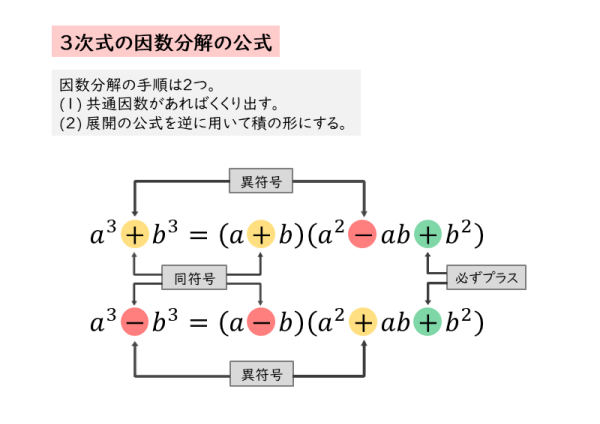
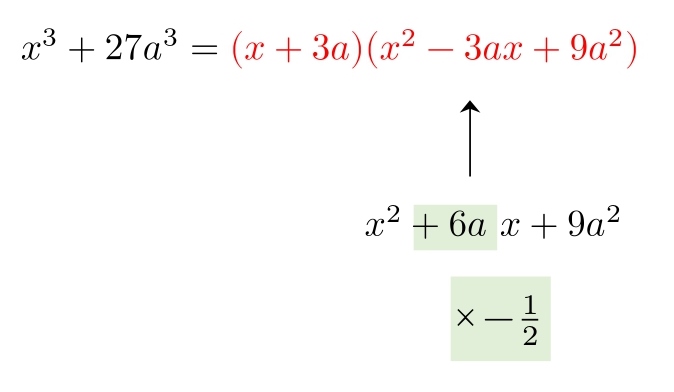
因数分解 3次式 公式-本問の因数分解を複素数の範囲まで進めると, $\omega$ を $1$ の虚数立方根の $1$ つとして, \\begin{aligned} &x^3y^3z^33xyz \\ &= (xyz)(x\omega y\omega ^2z)(x\omega ^2y\omega z) \end{aligned}\ となる この因数分解は, $3$ 次方程式の「オイラーの解法」に利用される 例えば, $3 因数分解～基礎から応用まで 高校の数学では，最初に「数と式」という分野を学習します（数学 i ）。 ここでは、単項式や多項式、それに整式、式の展開公式などを学びますが、その次に待ち受けているのが「因数分解」です。 因数分解は、数学 i だけでなく今後の数学でずっと登場す
因数分解 3次式 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
 |  |  |
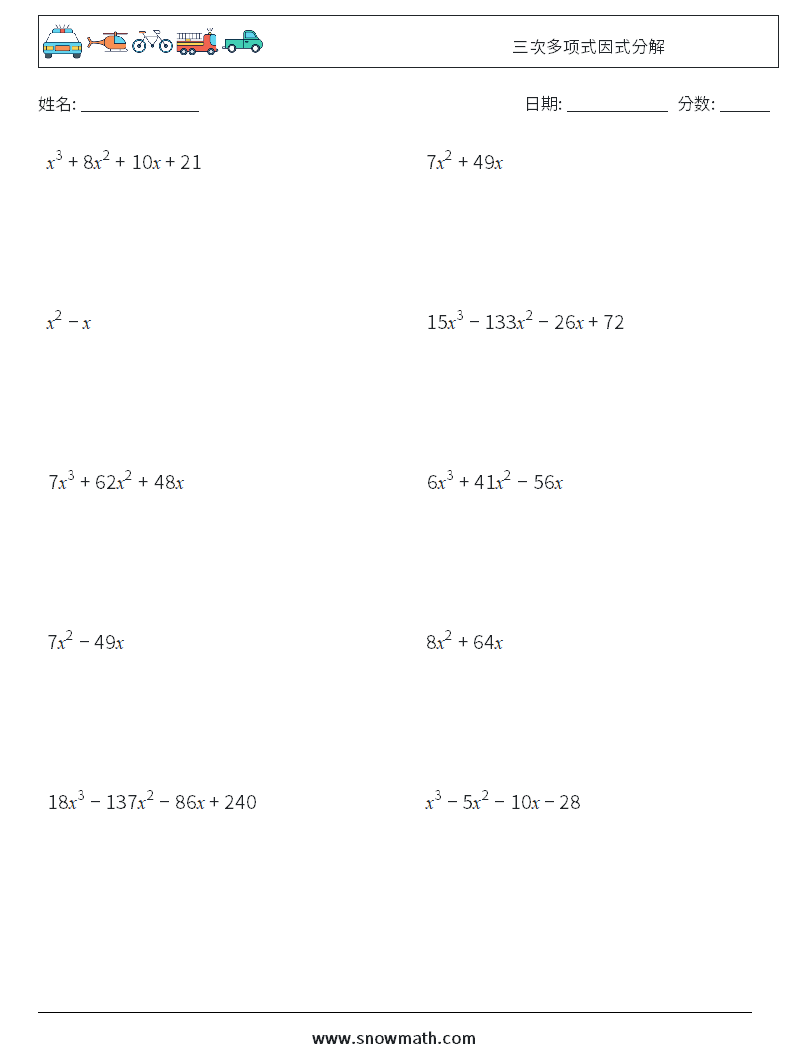「因数分解 3次式 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
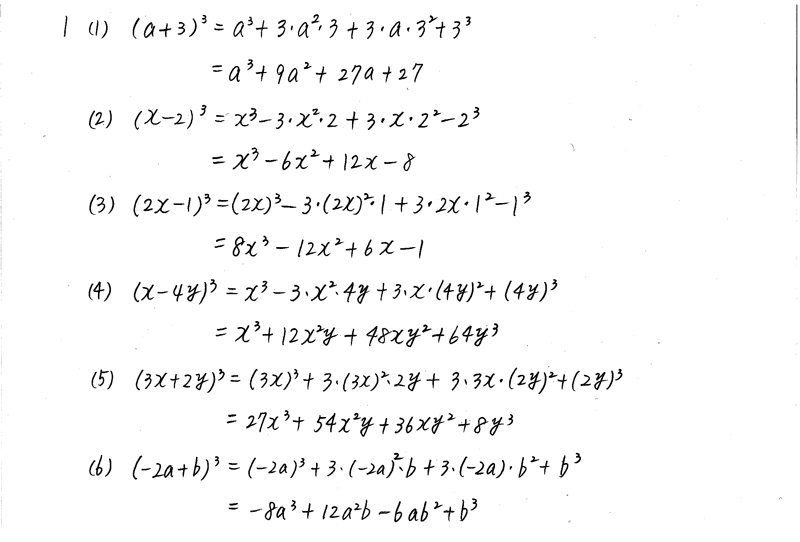「因数分解 3次式 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「因数分解 3次式 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
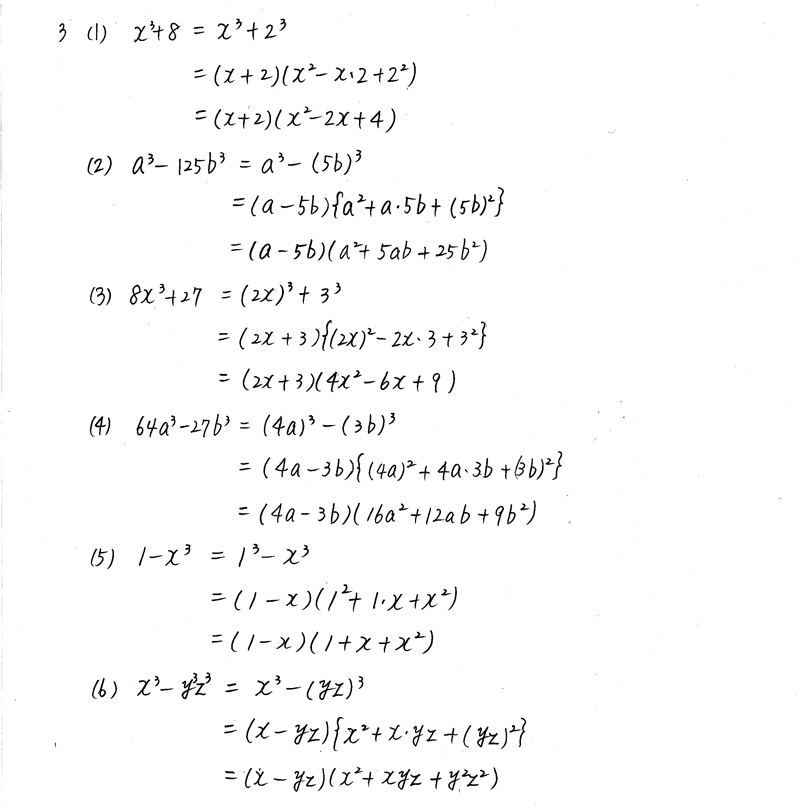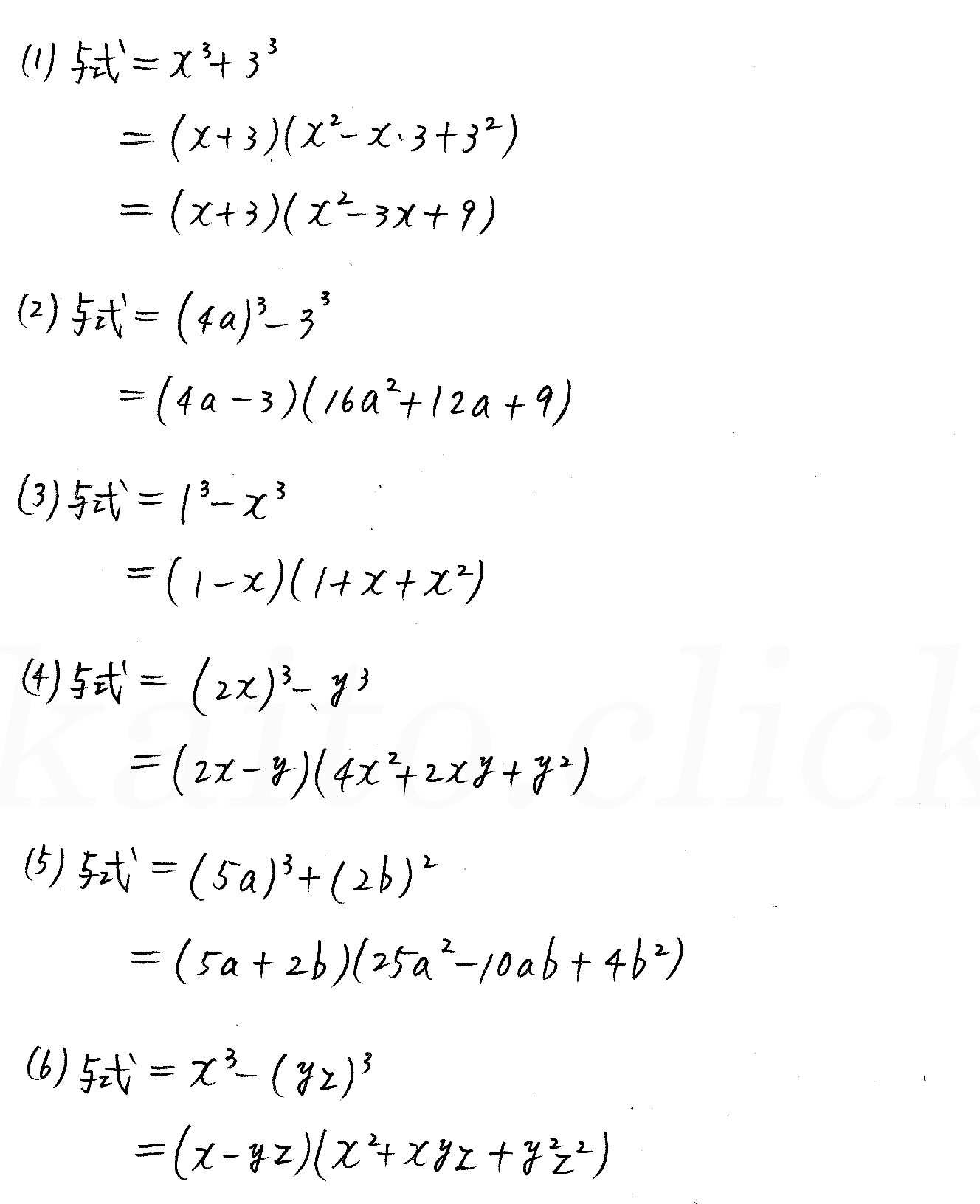「因数分解 3次式 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
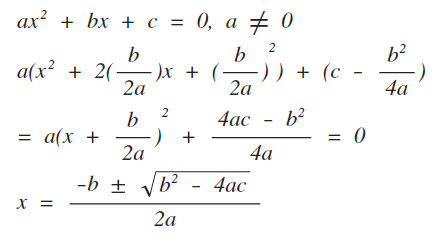「因数分解 3次式 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | -2.png "质因数分解 3位数 儿童数学练习国小国中数学练习题题库下载列印 教学学习解答") | |
 |  | |
 |  |  |
 |  | |
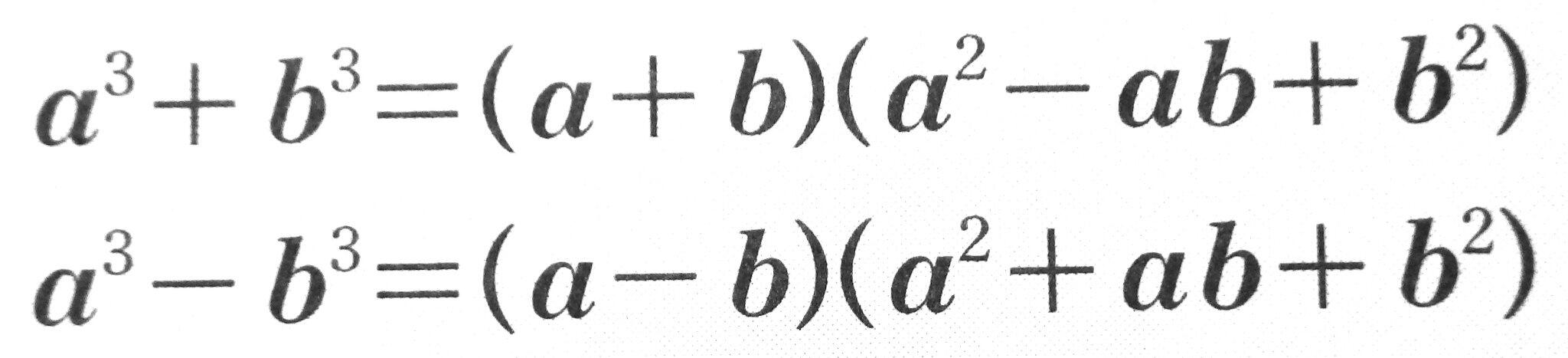「因数分解 3次式 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
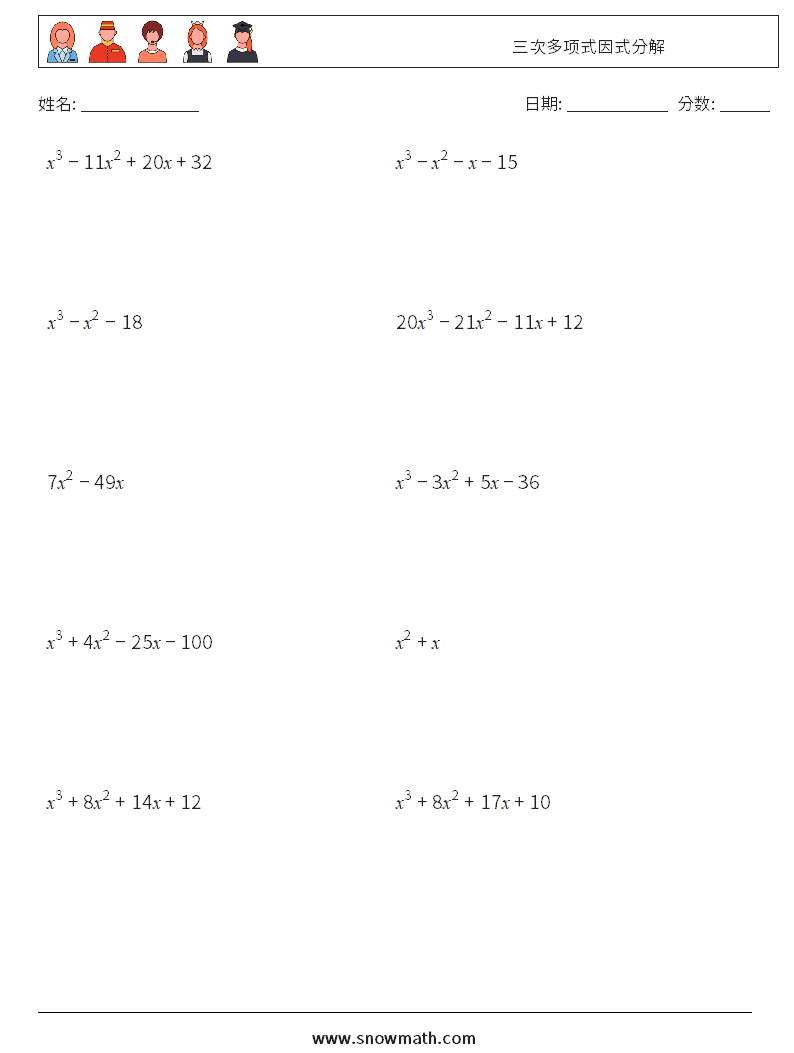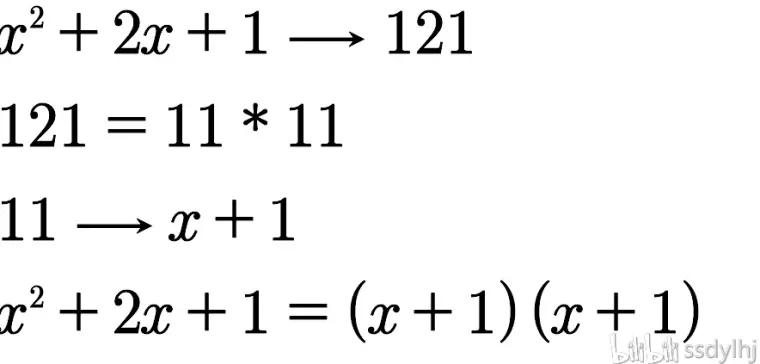 | -1.png 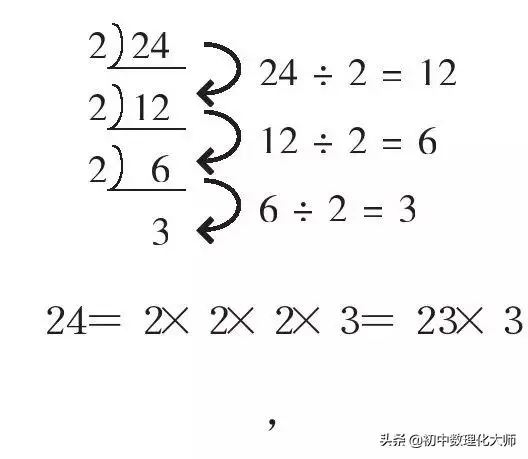"质因数分解 3位数 儿童数学练习国小国中数学练习题题库下载列印 教学学习解答") |  |
「因数分解 3次式 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
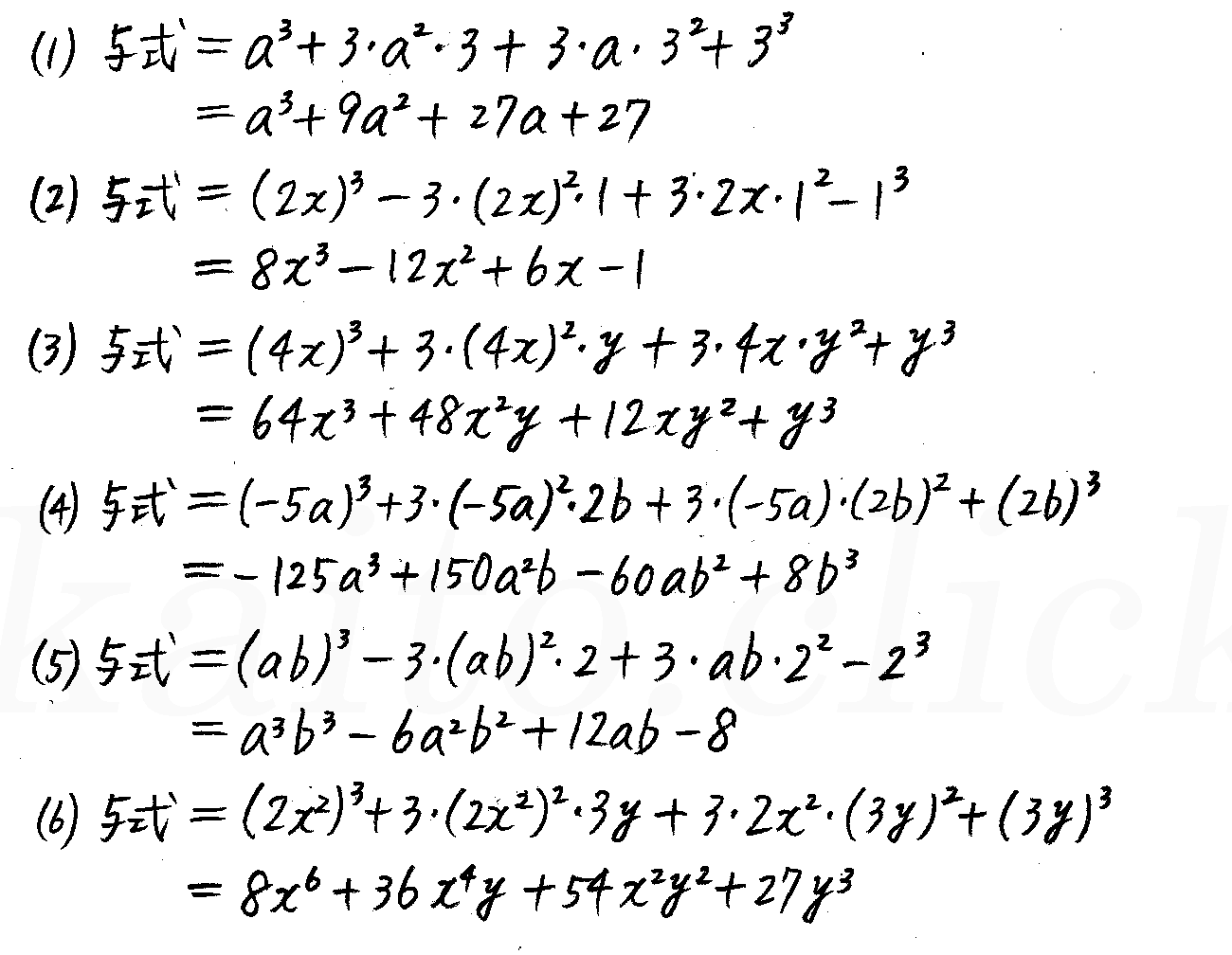「因数分解 3次式 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
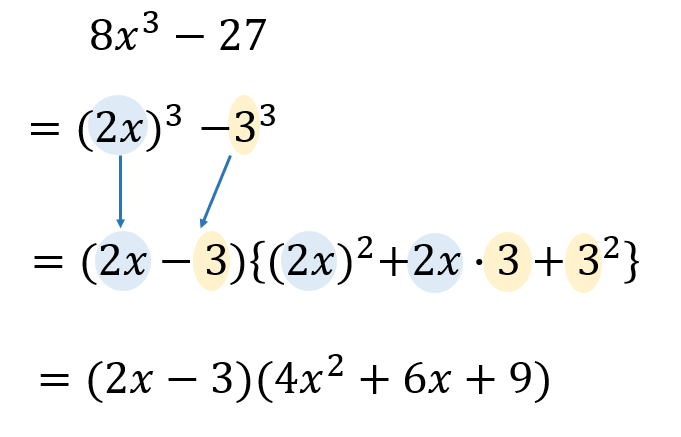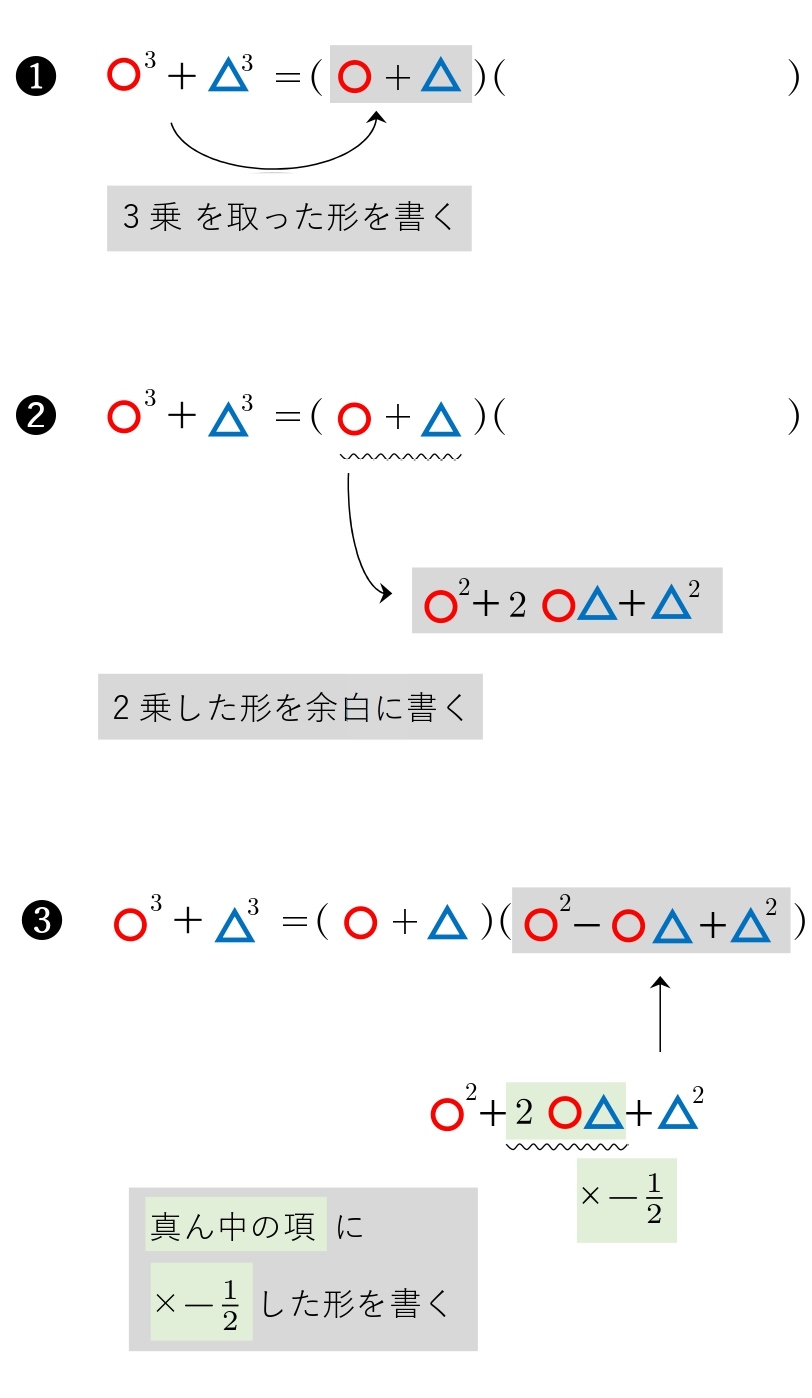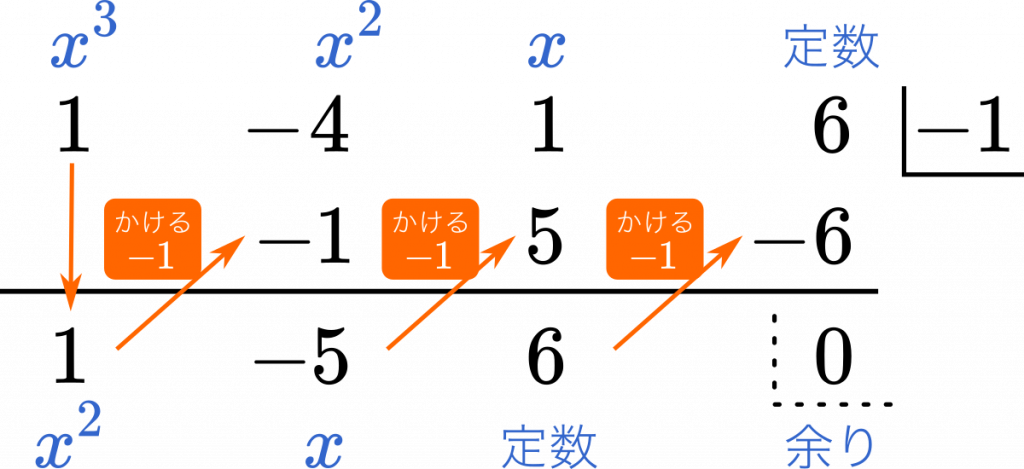
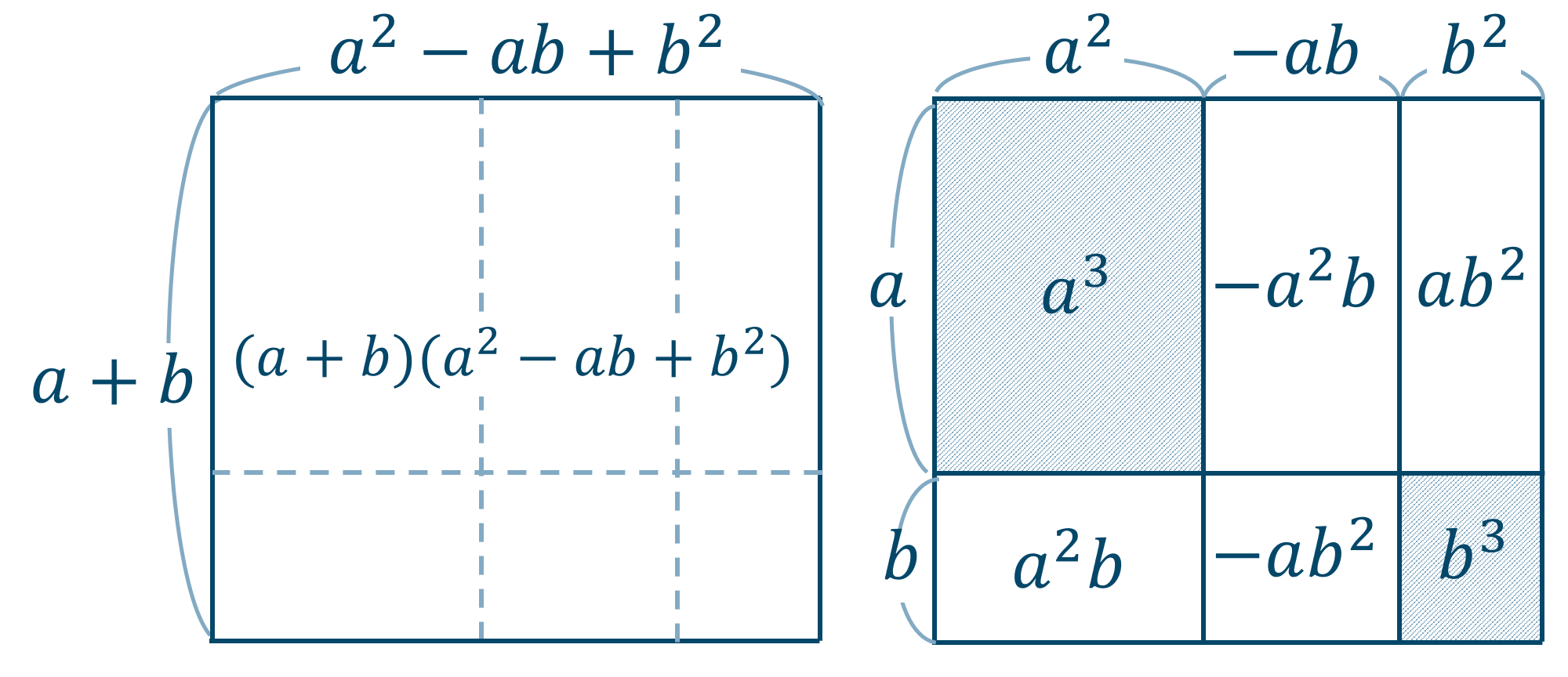
3次式の因数分解の問題では，単に展開公式を逆に使うだけの問題もありますが，2次式の因数分解と異なり，公式の使い方がややこしくなることがあります。 3次関数面積を求める12分の1公式の証明とその使い方 part2 解き方① 三次式の因数分解の公式を使う 三次式の因数分解の公式を利用して三次方程式を因数分解する方法を説明します。 例題 を解きなさい。 STEP1 (左辺) = 0 の形にする 右辺に何か数値がある場合は、すべて左辺に移項して 左辺 の形にします
Incoming Term: 因数分解 3次式, 因数分解 3次式 公式,
0 件のコメント:
コメントを投稿